AES 256 titkosítás

ÁltalánosTervezőkJoan Daemen, Vincent RijmenElőször megjelent1998SzármaztatottTérUtódokAnubisz, Grand Cru, KalynaTanúsításAES győztes, CRYPTREC, NESSIE, NSARejtjel részletKulcsméretek128, 192 vagy 256 bit^{[1. megjegyzés]}Blokkméretek128 bit^{[2. megjegyzés]}SzerkezetHelyettesítési–permutációs hálózatFordulók10, 12 vagy 14 (a kulcs méretétől függően)Legjobb nyilvános kriptoanalízis

Olyan támadásokat tettek közzé, amelyek számításilag gyorsabbak, mint egy teljes brute-force támadás, bár 2023-ig egyik sem kivitelezhető számításilag.^[1]Az AES-128 esetében a kulcs visszaállítható a számítási bonyolultság 2-ből^126.1 használata a biklikettámadás. Az AES-192 és AES-256 elleni biklikk támadások esetén a számítási bonyolultság 2^189,7 és 2^254,4 illetve alkalmazni. Kapcsolódó kulcsú támadások 2-es bonyolultsággal képes megtörni az AES-192-t és az AES-256-ot^99.5 és 2¹⁷⁶ időben és adatban egyaránt, illetve.^[2]

Újabb támadást írtak blogra^[3] és kiadták, mint a preprint^[4] 2009-ben. Ez a támadás az AES-256 ellen irányul, amely csak két kapcsolódó kulcsot és 2-t használ³⁹ ideje helyreállítani a 9 körös verzió teljes 256 bites kulcsát, vagy 2⁴⁵ ideje egy 10 körös verziónak erősebb típusú kapcsolódó alkulcsos támadással, vagy 2⁷⁰ 11 körös változat ideje.

Az A Fejlett titkosítási szabvány (AES), eredeti nevén is ismert Rijndael (Holland kiejtés: [ˈrɛindaːl]),^[5] egy specifikáció a titkosítás az Egyesült Államok által létrehozott elektronikus adatokról. Nemzeti Szabványügyi és Technológiai Intézet (NIST) 2001-ben.^[6]

Az AES a Rijndael egyik változata blokk titkosítás^[5] kettes által kifejlesztett Belga kriptográfusok, Joan Daemen és Vincent Rijmen, aki javaslatot nyújtott be^[7] a NIST-nek a AES kiválasztási folyamat.^[8] A Rijndael a különböző titkosítások családja kulcs és blokkméretek. Az AES-hez a NIST a Rijndael család három tagját választotta ki, mindegyik blokkmérete 128 bit, de három különböző kulcshossz: 128, 192 és 256 bit.

Az AES-t elfogadta a amerikai kormány. Felülírja a Adattitkosítási szabvány (DES),^[9] amely 1977-ben jelent meg. Az AES által leírt algoritmus a szimmetrikus kulcsú algoritmus, ami azt jelenti, hogy ugyanazt a kulcsot használják az adatok titkosításához és visszafejtéséhez.

Az Egyesült Államokban az AES-t a NIST US néven jelentette be. FIPS PUB 197 (FIPS 197) 2001. november 26-án.^[6] Ez a bejelentés egy ötéves szabványosítási folyamatot követett, amelynek során tizenöt egymással versengő tervet mutattak be és értékeltek, mielőtt a Rijndael titkosítást választották a legmegfelelőbbnek.^{[3. megjegyzés]}

Az AES benne van a ISO/IEC 18033-3 standard. Az AES az Egyesült Államok szövetségi kormányának szabványaként 2002. május 26-án lépett hatályba, miután az Egyesült Államok jóváhagyta. Kereskedelmi miniszter Donald Evans. Az AES számos különböző titkosítási csomagban elérhető, és ez az első (és egyetlen) nyilvánosan elérhető rejtjelez az Egyesült Államok jóváhagyta. Nemzetbiztonsági Ügynökség (NSA) számára szigorúan titkos információ, ha NSA által jóváhagyott kriptográfiai modulban használják.^{[4. megjegyzés]}

Az Advanced Encryption Standard (AES) a következők mindegyikében van meghatározva

• FIPS PUB 197: Advanced Encryption Standard (AES)^[6]
• ISO/IEC 18033-3: Blokk titkosítások^[10]

Az AES egy tervezési elven alapul, amelyet a szubsztitúciós–permutációs hálózat, és hatékony mind szoftverben, mind hardverben.^[11] Elődjétől, a DES-től eltérően az AES nem használ a Feistel hálózat. Az AES a Rijndael egy változata, fix blokk mérete 128-ból bitek, és a kulcsméret 128, 192 vagy 256 bites. Ezzel szemben Rijndael per se blokk- és kulcsméretekkel van megadva, amelyek a 32 bit tetszőleges többszörösei lehetnek, legalább 128 és legfeljebb 256 bittel. A legtöbb AES számítást egy adott területen végzik véges mező.

Az AES 4 × 4-en működik oszlop-főrend 16 bájtos tömb b₀,b₁,…,b₁₅    nevezett a állam:^{[5. megjegyzés]}

[b0b4b8b12b1b5b9b13b2b6b10b14b3b7b11b15]

Az AES titkosításhoz használt kulcsméret megadja a bemenetet konvertáló transzformációs körök számát, az úgynevezett egyszerű szöveg, a végső kimenetbe, az úgynevezett rejtjelezett szöveg. A fordulók száma a következő:

• 10 kör 128 bites kulcsokhoz.
• 12 kör 192 bites kulcsokhoz.
• 14 kör 256 bites kulcsokhoz.

Minden kör több feldolgozási lépésből áll, köztük egy olyanból, amely magától a titkosítási kulcstól függ. Fordított körök készletét alkalmazzák a rejtjelezett szöveg visszaalakítására az eredeti egyszerű szöveggé ugyanazon titkosítási kulcs használatával.

1. KeyExpansion A – kerek kulcsok a rejtjelkulcsból származnak a AES kulcs ütemezése. Az AES minden körhöz külön 128 bites kerek kulcsblokkot igényel, plusz még egyet.
2. Kezdeti kerek kulcs kiegészítés:
   1. AddRoundKey – az állapot minden bájtját a kerek kulcs bájtjával kombináljuk bitenkénti xor.
3. 9, 11 vagy 13 forduló:
   1. SubBytes – a nemlineáris helyettesítési lépés, ahol minden bájtot egy másikra cserélünk a keresőtábla.
   2. ShiftRows – egy transzponálási lépés, ahol az állapot utolsó három sora ciklikusan eltolódik bizonyos számú lépésben.
   3. MixColumns – egy lineáris keverési művelet, amely az állapot oszlopain működik, és minden oszlopban egyesíti a négy bájtot.
   4. AddRoundKey
4. Utolsó kör (összesen 10, 12 vagy 14 körből áll):
   1. SubBytes
   2. ShiftRows
   3. AddRoundKey

A ban SubBytes lépés, minden bájt ai,j a állam tömböt a SubByte S(ai,j) 8 bites használata helyettesítő doboz. A 0. forduló előtt a állam a tömb egyszerűen az egyszerű szöveg/bemenet. Ez a művelet biztosítja a nemlinearitást a rejtjelez. A használt S-box a multiplikatív inverz át GF(2⁸), ismert, hogy jó nemlinearitási tulajdonságokkal rendelkezik. Az egyszerű algebrai tulajdonságokon alapuló támadások elkerülése érdekében az S-boxot úgy állítják elő, hogy az inverz függvényt egy invertálhatóval kombinálják affin transzformáció. Az S-box is úgy van megválasztva, hogy elkerülje a rögzített pontokat (és így van a zavar), azaz S(ai,j)≠ai,j, és bármely ellentétes fix pont is, azaz S(ai,j)⊕ai,j≠FF16. A visszafejtés végrehajtása közben a InvSubBytes lépés (az inverze SubBytes) használatos, amihez először az affin transzformáció inverzét kell venni, majd meg kell találni a multiplikatív inverzt.

Az A ShiftRows a Step az állapot sorain működik; ciklikusan eltolja az egyes sorok bájtjait egy bizonyossal eltolódás. Az AES esetében az első sor változatlan marad. A második sor minden bájtja eggyel balra tolódik. Hasonlóképpen, a harmadik és a negyedik sort kettő, illetve három eltolás tolja el.^{[6. megjegyzés]} Ily módon a kimeneti állapot minden oszlopa a ShiftRows a lépés a bemeneti állapot minden oszlopának bájtjaiból áll. Ennek a lépésnek az a fontossága, hogy elkerüljük az oszlopok önálló titkosítását, ebben az esetben az AES négy független blokkrejtjellé fajulna.

A ban MixColumns lépésként az állapot minden oszlopának négy bájtját egy invertálható segítségével egyesítjük lineáris transzformáció. Az A MixColumns a függvény négy bájtot vesz bemenetként, és négy bájtot ad ki, ahol minden bemeneti bájt mind a négy kimeneti bájtra hatással van. Együtt ShiftRows, MixColumns ellát diffúzió a rejtjelben.

A művelet során minden oszlopot egy rögzített mátrix segítségével transzformálunk (az oszloppal balra szorzott mátrix új oszlopértéket ad az állapotban):

[b0,jb1,jb2,jb3,j]=[2311123111233112][a0,ja1,ja2,ja3,j]0≤j≤3

A mátrixszorzás a bejegyzések szorzásából és összeadásából áll. A bejegyzések a sorrendi polinom együtthatóiként kezelt bájtok x7. A kiegészítés egyszerűen XOR. A szorzás modulo irreducibilis polinom x8+x4+x3+x+1. Ha bitről bitre dolgozzuk fel, akkor eltolás után feltételes XOR 1b-vel₁₆ akkor kell végrehajtani, ha az eltolt érték nagyobb, mint FF₁₆ (a túláramlást a generáló polinom kivonásával kell korrigálni). Ezek a szokásos szorzás speciális esetei GF⁇(28).

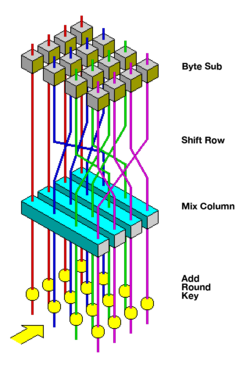
Általánosabb értelemben minden oszlopot polinomként kezelünk GF⁇(28)és ezután modulo-t szoroznak 0116⋅z4+0116egy rögzített polinommal c(z)=0316⋅z3+0116⋅z2+0116⋅z+0216. Az együtthatók a sajátjukban jelennek meg hexadecimális a bitpolinomok bináris reprezentációjának megfelelője GF⁇(2)[x]. Az A MixColumns a lépés a bemutatott adott szorzásaként is felfogható MDS mátrix a véges mező GF⁇(28). Ezt a folyamatot a cikk részletesebben ismerteti Rijndael MixOszlopok.

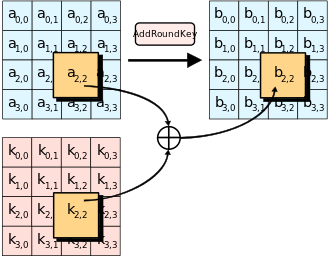
A ban AddRoundKey lépés, az alkulcsot kombináljuk az állapottal. Minden körhöz egy alkulcs származik a főből kulcs használata Rijndael legfontosabb menetrendje; minden alkulcs mérete megegyezik az állapottal. Az alkulcsot úgy adjuk hozzá, hogy az állapotot az alkulcs megfelelő bájtjával bitenként kombináljuk XOR.

A 32 bites vagy nagyobb szavakat tartalmazó rendszereken a titkosítás végrehajtásának felgyorsítása lehetséges a SubBytes és ShiftRows lépésekkel a MixColumns lépj úgy, hogy átalakítod őket táblázatkeresések sorozatává. Ehhez négy 256 bejegyzésből álló 32 bites táblázatra van szükség (együtt 4096 bájtot foglalnak el). Ezután egy kör végrehajtható 16 táblázatkeresési művelettel és 12 32 bites kizárólagos vagy művelettel, majd négy 32 bites kizárólagos vagy művelettel a AddRoundKey lépés.^[12] Alternatív megoldásként a táblázatkeresési művelet végrehajtható egyetlen 256 bejegyzésből álló 32 bites táblával (1024 bájtot foglalva), amelyet körkörös forgatási műveletek követnek.

Bájtorientált megközelítéssel kombinálható a SubBytes, ShiftRows, és MixColumns lépések egyetlen körös műveletbe.^[13]

Az A Nemzetbiztonsági Ügynökség (NSA) áttekintette az AES összes döntősét, beleértve Rijndaelt is, és kijelentette, hogy mindegyik elég biztonságos az Egyesült Államok számára. Kormányzati nem minősített adatok. 2003 júniusában az Egyesült Államok. A kormány bejelentette, hogy az AES-t fel lehet használni a védelemre minősített információ:

Az AES algoritmus összes kulcshosszának (azaz a 128-as, 192-es és 256-os) kialakítása és erőssége elegendő a minősített információk TITKOS szintig történő védelméhez. A SZIGORÚAN TITKOS információkhoz a 192-es vagy a 256-os kulcshosszt kell használni. Az AES-nek a nemzetbiztonsági rendszerek és/vagy információk védelmét szolgáló termékekben történő bevezetését az NSA-nak felül kell vizsgálnia és hitelesítenie kell beszerzésük és felhasználásuk előtt.^[14]

Az AES 10 kört tartalmaz a 128 bites kulcsokhoz, 12 kört a 192 bites kulcsokhoz és 14 kört a 256 bites kulcsokhoz.

Kriptográfusoknak, a kriptografiai a „törés“ minden gyorsabb, mint a brute-force támadás—azaz egy próba visszafejtés végrehajtása minden lehetséges kulcshoz egymás után (lát Cryptanalysis § Számítási erőforrások szükségesek). A szünet tehát olyan eredményeket tartalmazhat, amelyek a jelenlegi technológiával megvalósíthatatlanok. Annak ellenére, hogy nem praktikusak, az elméleti szünetek néha betekintést nyújthatnak a sebezhetőségi mintákba. A legnagyobb sikeres, nyilvánosan ismert brute force támadás egy széles körben megvalósított blokk-rejtjel titkosítási algoritmus ellen egy 64 bites ellen irányult RC5 kulcs által elosztott.net 2006-ban.^[15]  

A kulcstér 2-szeresére nő minden további kulcshosszúság bit után, és ha a kulcs minden lehetséges értéke kiegyenlíthető; ez az átlagos brute-force kulcskeresési idő megduplázódását jelenti minden további kulcshosszúság bittel. Ez azt jelenti, hogy a nyers erejű keresés erőfeszítése exponenciálisan növekszik a kulcs hosszával. A kulcshossz önmagában nem jelent biztonságot a támadások ellen, mivel vannak nagyon hosszú kulcsú titkosítások, amelyeket sebezhetőnek találtak.

Az AES meglehetősen egyszerű algebrai kerettel rendelkezik.^[16] 2002-ben egy elméleti támadás, a „neveXSL támadás„, jelentette be Nicolas Courtois és Josef Pieprzyk, amely az AES algoritmus gyengeségét mutatja, részben a nemlineáris komponensek alacsony összetettsége miatt.^[17] Azóta más lapok kimutatták, hogy a támadás, ahogy eredetileg bemutatták, kivitelezhetetlen; lát XSL támadás blokk titkosítások ellen.

Az AES kiválasztási folyamata során a versengő algoritmusok fejlesztői azt írták Rijndael algoritmusáról, hogy „aggódunk [annak] használata miatt… a biztonság szempontjából kritikus alkalmazásokban“^[18] 2000 októberében azonban az AES kiválasztási folyamat végén a Bruce Schneier, a versengő algoritmus fejlesztője Kétszeres, azt írta, hogy bár úgy gondolta, hogy egy napon sikeres tudományos támadásokat fognak kidolgozni Rijndael ellen, „nem hitte el, hogy bárki valaha is felfedezne egy támadást, amely lehetővé tenné, hogy valaki elolvassa a Rijndael forgalmat“^[19]

2006-ra a legismertebb támadások a 128 bites kulcsok 7, a 192 bites kulcsok 8 és a 256 bites kulcsok 9 köre volt.^[20]

2009 májusáig az egyetlen sikeres közzétett támadás a teljes AES ellen az volt oldalcsatornás támadások néhány konkrét megvalósításon. 2009-ben egy új kapcsolódó-kulcs támadás felfedezték, hogy kihasználja az AES kulcsfontosságú ütemezésének egyszerűségét, és összetettsége 2¹¹⁹. 2009 decemberében 2-re javították^99.5.^[2] Ez egy 2009-ben korábban felfedezett támadás folytatása Alex Birjukov, Dmitrij Khovratovics, és Ivica Nikolić, 2-es összetettséggel⁹⁶ minden 2-ből egynek³⁵ kulcsok.^[21] A kapcsolódó kulcsú támadások azonban egyetlen megfelelően megtervezett kriptográfiai protokollban sem jelentenek aggodalmat, mivel egy megfelelően megtervezett protokoll (azaz implementációs szoftver) ügyelni fog arra, hogy ne engedélyezze a kapcsolódó kulcsokat, lényegében azáltal, hogy megszorító a támadó eszköze a kulcsok kiválasztására a rokonság szempontjából.

Újabb támadást írt blogba Bruce Schneier^[3] 2009. július 30-án, és a preprint^[22] 2009. augusztus 3-án. Alex Birjukov új támadása, Orr Dunkelman, Nathan Keller, Dmitrij Khovratovics, és Adi Shamir, az AES-256 ellen szól, amely csak két kapcsolódó kulcsot és 2-t használ³⁹ ideje helyreállítani a 9 körös verzió teljes 256 bites kulcsát, vagy 2⁴⁵ ideje egy 10 körös verziónak erősebb típusú kapcsolódó alkulcsos támadással, vagy 2⁷⁰ idő egy 11 körös verzióhoz.256 bites AES 14 kört használ, így ezek a támadások nem hatékonyak a teljes AES ellen.

Ezeknek a támadásoknak a gyakorlatiasságát erősebb kapcsolódó kulcsokkal kritizálták,^[23] például az AES-128 elleni választott kulcs-kapcsolatokról szóló tanulmány, amelyet Vincent Rijmen írt 2010-ben.^[24]

2009 novemberében az első ismert kulcs megkülönböztető támadás az AES-128 csökkentett, 8 körös változata előnyomatként jelent meg.^[25] Ez az ismert kulcs megkülönböztető támadás a visszapattanás vagy a középről induló támadás javítása az AES-szerű permutációk ellen, amelyek két egymást követő permutációs kört egy úgynevezett Super-S-box alkalmazásának tekintenek. Az AES-128 8 körös változatán működik, 2-es időkomplexitással⁴⁸, és a memória összetettsége 2³². A 128 bites AES 10 kört használ, így ez a támadás nem hatékony a teljes AES-128 ellen.

Az első kulcs-helyreállítási támadások a teljes AES-t Andrej Bogdanov, Dmitrij Khovratovics és Christian Rechberger készítette, és 2011-ben adták ki.^[26] A támadás a biklikettámadás és körülbelül négyszeresére gyorsabb, mint a nyers erő. 2 kell hozzá^126.2 műveletek az AES-128 kulcs helyreállításához. Az AES-192 és AES-256 esetében 2^190.2 és 2^254,6 műveletekre van szükség, illetve. Ezt az eredményt tovább javították 2-re^126,0 az AES-128 esetében 2^189,9 az AES-192 és 2 esetében^254.3 biaoshuai Tao és Hongjun Wu AES-256-hoz egy 2015-ös tanulmányában,^[27]melyek a jelenlegi legjobb eredmények az AES elleni kulcsfontosságú helyreállítási támadásban.

Ez egy nagyon kis nyereség, mivel egy 126 bites kulcs (128 bit helyett) még mindig több milliárd évbe telne, hogy brutális erőt fejtsen ki a jelenlegi és előrelátható hardverre. Ezenkívül a szerzők a technikájukkal kiszámítják a legjobb támadást az AES-en egy 128 bites kulccsal, amely 2 tárolását igényli⁸⁸ az adatok bitjei. Ez körülbelül 38 billió terabájtnyi adatot jelent, ami több volt, mint a bolygó összes számítógépén tárolt összes adat 2016-ban.^[28] Egy 2015-ös tanulmány később 2-re javította a tér bonyolultságát⁵⁶ bitek,^[27] ami 9007 terabájt (miközben továbbra is körülbelül 2-es időbonyolultságot tart fenn¹²⁶).

A szerint a Snowden dokumentumok, az NSA kutatásokat végez arra vonatkozóan, hogy egy kriptográfiai támadás alapján tau statisztika segíthet az AES megtörésében.^[29]

Jelenleg nem ismert olyan gyakorlati támadás, amely lehetővé tenné, hogy valaki a kulcs ismerete nélkül beolvassa az AES által titkosított adatokat, ha azokat helyesen implementálják.^{[idézet szükséges]}

Oldalcsatornás támadások ne támadja meg a rejtjelet a fekete doboz, és így nem kapcsolódnak a klasszikus kontextusban meghatározott titkosítási biztonsághoz, hanem a gyakorlatban fontosak. Megtámadják a titkosítás olyan hardver- vagy szoftverrendszereken történő megvalósítását, amelyek véletlenül adatokat szivárogtatnak ki. Számos ilyen ismert támadás létezik az AES különféle megvalósításai ellen.

2005 áprilisában, D. J. Bernstein bejelentett egy gyorsítótár-időzítési támadást, amellyel megtörte a használt egyéni szervert OpenSSLAz AES titkosítás.^[30] A támadáshoz több mint 200 millió kiválasztott egyszerű szövegre volt szükség.^[31] Az egyedi szervert úgy tervezték, hogy a lehető legtöbb időzítési információt adja ki (a szerver a titkosítási művelet által felvett gépi ciklusok számát jelenti). Azonban, ahogy Bernstein rámutatott, „a szerver időbélyegeinek pontosságának csökkentése, vagy a szerver válaszaiból való kiiktatása nem állítja meg a támadást: a kliens egyszerűen oda-vissza időzítéseket használ a helyi órája alapján, és a megnövekedett zajt kompenzálja nagyobb számú minta átlagolásával.“^[30]

2005 októberében Dag Arne Osvik, Adi Shamir és Eran Tromer bemutatott egy tanulmányt, amely számos gyorsítótár-időzítési támadást mutatott be az OpenSSL-ben és a Linuxban található AES-megvalósítások ellen dm-crypt partíció titkosítási funkció.^[32] Egy támadásnak sikerült egy teljes AES-kulcsot megszereznie mindössze 800 titkosítást kiváltó művelet után, összesen 65 ezredmásodperc alatt. Ez a támadás megköveteli, hogy a támadó képes legyen programokat futtatni ugyanazon a rendszeren vagy platformon, amely AES-t hajt végre.

2009 decemberében támadást tettek közzé néhány használt hardvermegvalósítás ellen differenciálhiba elemzés és lehetővé teszi egy 2-es összetettségű kulcs helyreállítását³².^[33]

2010 novemberében Bangerter Endre, David Gullasch és Stephan Krenn publikált egy tanulmányt, amely gyakorlati megközelítést írt le a titkos kulcsok AES-128-ból való „közel valós idejű“ helyreállításához anélkül, hogy titkosított szövegre vagy egyszerű szövegre lenne szükség. A megközelítés a tömörítési táblázatokat használó AES-128 megvalósításokon is működik, mint például az OpenSSL.^[34] Néhány korábbi támadáshoz hasonlóan ez is megköveteli a jogosulatlan kód futtatásának lehetőségét az AES titkosítást végrehajtó rendszeren, ami sokkal könnyebben elérhető rosszindulatú programok fertőzésével, mint a root fiók parancsolgatása.^[35]

2016 márciusában C. Ashokkumar, Ravi Prakash Giri és Bernard Menezes egy oldalcsatornás támadást mutatott be az AES-megvalósítások ellen, amelyek képesek visszaállítani a teljes 128 bites AES-kulcsot mindössze 6–7 egyszerű szöveg/rejtjelezett szöveg blokkban, ami jelentős előrelépés a korábbi munkákhoz képest, amelyek 100 és egymillió közötti titkosítást igényel.^[36] A javasolt támadáshoz szabványos felhasználói jogosultságokra és kulcs-visszakereső algoritmusokra van szükség, amelyek egy perc alatt futnak.

Számos modern CPU beépített hardver utasítások az AES-hez, amelyek védenek az időzítéssel kapcsolatos oldalcsatornás támadások ellen.^[37][38]

Az AES-256-ot annak tekintik kvantumálló, mivel hasonló kvantumellenállással rendelkezik, mint az AES-128 ellenállása a hagyományos, nem kvantumos támadásokkal szemben a 128-nál a biztonság bitjei. Az AES-192 és az AES-128 kisebb kulcsméretük miatt nem tekinthető kvantumállónak. Az AES-192 erőssége 96 bit a kvantumtámadásokkal szemben, az AES-128 pedig 64 bit erősségű a kvantumtámadásokkal szemben, így mindkettő bizonytalan.^[39][40]

Az A Kriptográfiai modul érvényesítési program (CMVP) az Egyesült Államok kormánya közösen működteti Nemzeti Szabványügyi és Technológiai Intézet (NIST) Számítógép-biztonsági Osztály és a Kommunikációs biztonsági intézmény Kanada kormányának (CSE). A NIST számára hitelesített kriptográfiai modulok használata FIPS 140-2 az Egyesült Államok kormánya megköveteli minden olyan adat titkosítását, amely besorolása: Érzékeny, de nem minősített (SBU) vagy magasabb. Az NSTISSP #11, National Policy Governing Acquisition of Information Assurance: „A minősített információk védelmére szolgáló titkosítási termékeket az NSA tanúsítja, az érzékeny információk védelmére szolgáló titkosítási termékeket pedig a NIST FIPS 140-2 szerint.“^[41]

Kanada kormánya is javasolja a használatát FIPS 140 validált kriptográfiai modulok részlegeinek nem minősített alkalmazásaiban.

Bár a NIST 197-es kiadványa („FIPS 197“) az egyedi dokumentum, amely lefedi az AES algoritmust, a szállítók általában a FIPS 140 alatt közelítik meg a CMVP-t, és több algoritmust kérnek (például Háromágyas DES vagy SHA1) egyidejűleg érvényesítve. Ezért ritka, hogy olyan kriptográfiai modulokat találjanak, amelyek egyedileg FIPS 197 validáltak, és maga a NIST általában nem vesz igénybe időt a FIPS 197 validált modulok külön listázására nyilvános webhelyén. Ehelyett a FIPS 197 validálása általában csak „FIPS által jóváhagyott: AES“ jelölésként szerepel (egy adott FIPS 197 tanúsítványszámmal) a FIPS 140 validált kriptográfiai modulok jelenlegi listáján.

A kriptográfiai algoritmus érvényesítési programja (CAVP)^[42] lehetővé teszi az AES algoritmus helyes megvalósításának független érvényesítését. A sikeres érvényesítés eredményeként megjelenik a NIST-érvényesítések oldalon.^[43] Ez a tesztelés előfeltétele a FIPS 140-2 modul érvényesítésének. A sikeres CAVP-ellenőrzés azonban semmiképpen sem jelenti azt, hogy az algoritmust megvalósító kriptográfiai modul biztonságos. A FIPS 140-2 érvényesítését vagy az NSA külön jóváhagyását nem tartalmazó kriptográfiai modult az Egyesült Államok kormánya nem tekinti biztonságosnak, és nem használható kormányzati adatok védelmére.^[41]

A FIPS 140-2 validálása technikailag és pénzügyileg is kihívást jelent.^[44] Létezik egy szabványos tesztsorozat, valamint a forráskód-felülvizsgálat egy eleme, amelyet néhány héten keresztül kell átadni. E vizsgálatok jóváhagyott laboratóriumon keresztül történő elvégzésének költsége jelentős lehet (pl. jóval több USD30.000)^[44] és nem tartalmazza a modul megírásához, teszteléséhez, dokumentálásához és érvényesítéshez való előkészítéséhez szükséges időt. Az érvényesítést követően a modulokat újra be kell nyújtani és újra kell értékelni, ha bármilyen módon megváltoztatják őket. Ez az egyszerű papírmunka-frissítésektől, ha a biztonsági funkció nem változott, az újratesztelés lényegesebb sorozatáig változhat, ha a biztonsági funkciót befolyásolta a változás.

A tesztvektorok egy adott bemenethez és kulcshoz ismert titkosítások halmaza. A NIST az AES tesztvektorok referenciáját AES Known Answer Test (KAT) vektorokként osztja el.^{[7. megjegyzés]}

A nagy sebesség és az alacsony RAM-igény volt az AES kiválasztási folyamat kritériuma. Választott algoritmusként az AES jól teljesített a legkülönfélébb hardvereken, a 8 bitesektől kezdve intelligens kártyák nagy teljesítményű számítógépekhez.

A Pentium Pro, az AES titkosításhoz bájtonként (cpb) 18 órajel szükséges,^[45] körülbelül 11 MiB/s áteresztőképességnek felel meg egy 200 MHz-es processzor esetében.

Tovább Intel Core és AMD Ryzen Támogató CPU-k AES-NI utasításkészlet kiterjesztések, áteresztőképesség lehet több GiB/s.^[46] Egy Intel-en Westmere CPU, AES-NI-t használó AES titkosítás körülbelül 1,3 cpb-t vesz igénybe az AES-128 és 1,8 cpb-t az AES-256 esetében.^[47]

• AES működési módok
• Lemez titkosítás
• Örvény – hash függvény, amelyet Vincent Rijmen és Paulo SLM Barreto hozott létre
• Ingyenes és nyílt forráskódú szoftvercsomagok listája